AI 101
What are CNNs (Convolutional Neural Networks)?
Perhaps you’ve wondered how Facebook or Instagram is able to automatically recognize faces in an image, or how Google lets you search the web for similar photos just by uploading a photo of your own. These features are examples of computer vision, and they are powered by convolutional neural networks (CNNs). Yet what exactly are convolutional neural networks? Let’s take a deep dive into the architecture of a CNN and understand how they operate.
What are Neural Networks?
Before we begin talking about convolutional neural networks, let’s take a moment to define regular neural network. There’s another article on the topic of neural networks available, so we won’t go too deep into them here. However, to briefly define them they are computational models inspired by the human brain. A neural network operates by taking in data and manipulating the data by adjusting “weights”, which are assumptions about how the input features are related to each other and the object’s class. As the network is trained the values of the weights are adjusted and they will hopefully converge on weights that accurately capture the relationships between features.
This is how a feed-forward neural network operates, and CNNs are comprised of two halves: a feed-forward neural network and a group of convolutional layers.
What are Convolution Neural Networks (CNNs)?
What are the “convolutions” that happen in a convolutional neural network? A convolution is a mathematical operation that creates a set of weights, essentially creating a representation of parts of the image. This set of weights is referred to as a kernel or filter. The filter that is created is smaller than the entire input image, covering just a subsection of the image. The values in the filter are multiplied with the values in the image. The filter is then moved over to form a representation of a new part of the image, and the process is repeated until the entire image has been covered.
Another way to think about this is to imagine a brick wall, with the bricks representing the pixels in the input image. A “window” is being slid back and forth along the wall, which is the filter. The bricks that are viewable through the window are the pixels having their value multiplied by the values within the filter. For this reason, this method of creating weights with a filter is often referred to as the “sliding windows” technique.
The output from the filters being moved around the entire input image is a two-dimensional array representing the whole image. This array is called a “feature map”.
Why Convolutions are Essential
What is the purpose of creating convolutions anyway? Convolutions are necessary because a neural network has to be able to interpret the pixels in an image as numerical values. The function of the convolutional layers is to convert the image into numerical values that the neural network can interpret and then extract relevant patterns from. The job of the filters in the convolutional network is to create a two-dimensional array of values that can be passed into the later layers of a neural network, those that will learn the patterns in the image.
Filters And Channels
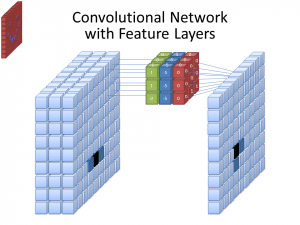
Photo: cecebur via Wikimedia Commons, CC BY SA 4.0 (https://commons.wikimedia.org/wiki/File:Convolutional_Neural_Network_NeuralNetworkFeatureLayers.gif)
CNNs don’t use just one filter to learn patterns from the input images. Multiple filters are used, as the different arrays created by the different filters leads to a more complex, rich representation of the input image. Common numbers of filters for CNNs are 32, 64, 128, and 512. The more filters there are, the more opportunities the CNN has to examine the input data and learn from it.
A CNN analyzes the differences in pixel values in order to determine the borders of objects. In a grayscale image, the CNN would only look at the differences in black and white, light-to-dark terms. When the images are color images, not only does the CNN take dark and light into account, but it has to take the three different color channels – red, green, and blue – into account as well. In this case, the filters possess 3 channels, just like the image itself does. The number of channels that a filter has is referred to as its depth, and the number of channels in the filter must match the number of channels in the image.
Convolutional Neural Network (CNN) Architecture
Let’s take a look at the complete architecture of a convolutional neural network. A convolutional layer is found at the beginning of every convolutional network, as it’s necessary to transform the image data into numerical arrays. However, convolutional layers can also come after other convolutional layers, meaning that these layers can be stacked on top of one another. Having multiple convolutional layers means that the outputs from one layer can undergo further convolutions and be grouped together in relevant patterns. Practically, this means that as the image data proceeds through the convolutional layers, the network begins to “recognize” more complex features of the image.
The early layers of a ConvNet are responsible for extracting the low-level features, such as the pixels that make up simple lines. Later layers of the ConvNet will join these lines together into shapes. This process of moving from surface-level analysis to deep-level analysis continues until the ConvNet is recognizing complex shapes like animals, human faces, and cars.
After the data has passed through all of the convolutional layers, it proceeds into the densely connected part of the CNN. The densely-connected layers are what a traditional feed-forward neural network looks like, a series of nodes arrayed into layers that are connected to one another. The data proceeds through these densely connected layers, which learns the patterns that were extracted by the convolutional layers, and in doing so the network becomes capable of recognizing objects.












