What are Neural Networks?

What are Artificial Neural Networks (ANNs)?

Many of the biggest advances in AI are driven by artificial neural networks. Artificial Neural Networks (ANNs) are the connection of mathematical functions joined together in a format inspired by the neural networks found in the human brain. These ANNs are capable of extracting complex patterns from data, applying these patterns to unseen data to classify/recognize the data. In this way, the machine “learns”. That’s a quick rundown on neural networks, but let’s take a closer look at neural networks to better understand what they are and how they operate.

Multi-layer Perceptron Explained

Before we look at more complex neural networks, we’re going to take a moment to look at a simple version of an ANN, a Multi-Layer Perceptron (MLP).

Imagine an assembly line at a factory. On this assembly line, one worker receives an item, makes some adjustments to it, and then passes it on to the next worker in the line who does the same. This process continues until the last worker in the line puts the finishing touches on the item and puts it on a belt that will take it out of the factory. In this analogy, there are multiple “layers” to the assembly line, and products move between layers as they move from worker to worker. The assembly line also has an entry point and an exit point.

A Multi-Layer Perceptron can be thought of as a very simple production line, made out of three layers total: an input layer, a hidden layer, and an output layer. The input layer is where the data is fed into the MLP, and in the hidden layer some number of “workers” handle the data before passing it onto the output layer which gives the product to the outside world. In the instance of an MLP, these workers are called “neurons” (or sometimes nodes) and when they handle the data they manipulate it through a series of mathematical functions.

Within the network, there are structures connecting node to node called “weights”. Weights are an assumption about how data points are related as they move through the network. To put that another way, weights reflect the level of influence that one neuron has over another neuron. The weights pass through an “activation function” as they leave the current node, which is a type of mathematical function that transforms the data. They transform linear data into non-linear representations, which enables the network to analyze complex patterns.

The analogy to the human brain implied by “artificial neural network” comes from the fact that the neurons which make up the human brain are joined together in a similar fashion to how nodes in an ANN are linked.

While multi-layer perceptrons have existed since the 1940s, there were a number of limitations that prevented them from being especially useful. However, over the course of the past couple of decades, a technique called “backpropagation” was created that allowed networks to adjust the weights of the neurons and thereby learn much more effectively. Backpropagation changes the weights in the neural network, allowing the network to better capture the actual patterns within the data.

Deep Neural Networks

Deep neural networks take the basic form of the MLP and make it larger by adding more hidden layers in the middle of the model. So instead of there being an input layer, a hidden layer, and an output layer, there are many hidden layers in the middle and the outputs of one hidden layer become the inputs for the next hidden layer until the data has made it all the way through the network and been returned.

The multiple hidden layers of a deep neural network are able to interpret more complex patterns than the traditional multilayer perceptron. Different layers of the deep neural network learn the patterns of different parts of the data. For instance, if the input data consists of images, the first portion of the network might interpret the brightness or darkness of pixels while the later layers will pick out shapes and edges that can be used to recognize objects in the image.

Different Types Of Neural Networks

There are various types of neural networks, and each of the various neural network types has its own advantages and disadvantages (and therefore their own use cases). The type of deep neural network described above is the most common type of neural network, and it is often referred to as a feedforward neural network.

One variation on neural networks is the Recurrent Neural Network (RNN). In the case of Recurrent Neural Networks, looping mechanisms are used to hold information from previous states of analysis, meaning that they can interpret data where the order matters. RNNs are useful in deriving patterns from sequential/chronological data. Recurrent Neural Networks can be either unidirectional or bidirectional. In the case of a bi-directional neural network, the network can take information from later in the sequence as well as earlier portions of the sequence. Since the bi-directional RNN takes more information into account, it’s better able to draw the right patterns from the data.

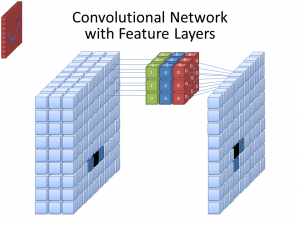
A Convolutional Neural Network is a special type of neural network that is adept at interpreting the patterns found within images. A CNN operates by passing a filter over the pixels of the image and achieving a numerical representation of the pixels within the image, which it can then analyze for patterns. A CNN is structured so that the convolutional layers which pull the pixels out of the image come first, and then the densely connected feed-forward layers come, those that will actually learn to recognize objects, come after this.